| Issue |
BIO Web Conf.
Volume 9, 2017
40th World Congress of Vine and Wine
|
|
|---|---|---|
| Article Number | 03020 | |
| Number of page(s) | 3 | |
| Section | Economy and Law | |
| DOI | https://doi.org/10.1051/bioconf/20170903020 | |
| Published online | 04 July 2017 | |
How intrinsic values influence wines prices
Corvinus University of Budapest, 1093
Budapest, Fővám tér 8., Hungary
The use of hedonic price indices is quite common in the wine economics literature, yet they mainly include scores of organoleptic tests and some dummy variables representing varieties and quality signs as geographical indications. This study focuses on the relation between the composition and the price of wines on the example of Hungarian wines. In Hungary, the wine law renders chemical analysis compulsory for all wines released to the market. The study includes five main compounds: actual alcoholic strength, total sugars, total acidity, sugar free extract and pH value and is based on hedonic price indices calculated on a sample of 2,453 wines. Results of several regressions – using different model specifications – consistently show that actual alcoholic strength, sugar content, sugar free extract and pH value are related with the price. Some characteristics have an optimal level, while in other cases the relation is linear.
© The Authors, published by EDP Sciences 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0 (http://creativecommons.org/licenses/by/4.0/).
This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0 (http://creativecommons.org/licenses/by/4.0/).
1. Introduction
The use of hedonic price indices is quite common in the literature of wine economics as these models explain differences in prices with variables describing the products’ intrinsic values.
The article is structured as follows. Section 2 presents an overview of the empirical literature, followed by a demonstration of methodology and data used in Sect. 3. Results are discussed and a graphical illustration of optimal values is provided in Sect. 4.
2. Literature on hedonic price indices
Rosen’s [1] basic model regards goods as an aggregate of their characteristics. Therefore, differences in prices reflect differences in the set of features. Later, several models were developed for the explanation of wine prices [2–8]. These studies mainly include scores of organoleptic tests and some dummy variables representing varieties and quality signs as geographical indications or the name of the producer. These models reveal the relation of these factors with prices, however do not consider the role of wine character.
Meanwhile, Lecocq and Visser [9] used data describing the weather of the vintage year for Bordeaux en primeur sales to confirm that weather data explain the changes in prices. However, in case of en primeur sales, when wines are far from being ready to be marketed and are to be aged for several additional months, weather data represent the most important information on quality for buyers – in addition to the name of the producer.
Combris et al. [10] developed several hedonic price index models on a sample of Burgundy wines. The most important results showed that some elements of the character (acidity, concentration and full-bodiedness) are significantly related to the price.
3. Sample and method
This study is based on hedonic price indices calculated on a sample of 2,453 wines. The prices were observed in the Hungarian off-trade sector (main wine shops and supermarkets). If a wine was observed on multiple sites, the lowest price was included in the dataset. The scope of the study extended only to wines, other grapevine products (such as sparkling wine) were excluded. Tokaj wine specialities were also excluded due to their relatively high concentration of nearly every compound in concern.
Creating a hedonic model using variables describing the characteristics of wines is quite rare as the availability of such data is highly limited. However, the Hungarian wine law imposes analytical tests on all wine products to be marketed. These tests include the measurement of the following compounds and indicators:
-
total and actual alcohol content,
-
free and bound sulphites,
-
pH value,
-
acidity (titratable, volatile),
-
density,
-
extract content (total and sugar free),
-
sugar content.
This study focuses on the most important compounds and indicators such as alcohol content, acidity, extract, sugar and pH. Data were provided by the national wine authority.
Descriptive statistics and measurement units are shown on Table 1. All prices were re-calculated for a unit of 0.75 l bottle.
Descriptive statistics. N=2,453.
The hedonic price indices calculated here are easily describable as follows: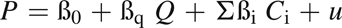 (1)where Q represents the actual quantity (lot size) of the wine and Ci represents the variable describing compound i
(1)where Q represents the actual quantity (lot size) of the wine and Ci represents the variable describing compound i
However, the basic model could not be applied using all right-hand side variables as some of them are interdependent. To avoid endogeneity, some pair of variables could not be present in the same model (for example: total alcohol vs. actual alcohol or pH vs. acidity).
Moreover, considering logarithms of some variables (price, in particular) resulted in better model fit, while including quadratic tags allowed to calculate optimal values. All in all, several regression models were run.
4. Results and discussion
Tables 2 and 3 summarise the results of the various regression models calculated.
Coefficients of models A-C and U.
Coefficients of models D-E.
As some of the variables observed are functions of each other (e.g. total alcohol content is virtually the sum of actual alcohol and sugar content), endogeneity would mean a major problem if all compounds were included in the same model. Therefore, four sets of models were calculated using whether total alcohol content or actual alcohol and sugar content and pH or acidity. As models using actual alcohol and sugar content with pH fitted the best, they are the sole to be presented here (except for the lin-lin specification, where the inclusion of acidity resulted in a better model).
As all models consistently show, the quantity and pH of wines are negatively related to the price. Other compounds (alcohol, sugar, acidity and sugar free extract) affect positively the price.
As comparing models A-C and D show, using a log-log specification resulted in the best fit.
However, all these models were possible to be improved by two ways.
On one hand, introducing quadratic tags resulted in a better (the best available) fit and the possibility to calculate optimum (model U), while on the other hand, differenti- ating between red and white wines helped to reveal the different role of sugar in red and white wines (model E).
As model U shows, the relation between prices and some compounds (actual alcohol and sugar) is not of linear nature. As the quadratic tag is significant, these compounds have an optimal level form the point of view of the price.
Meanwhile, model E confirms the different role of sugar in the case of red and white wines: while the more sugar, the more the price is for whites, the more sugar, the less the price is for reds. The effect is almost of the same extent, but to a different direction.
Estimations presented above showed that the variance of wine prices is due to differences of their chemical composition to a large extent (almost 60% in case of the best model).
It is up to further research to reveal the rest of the factors that influence wine prices.
References
- Rosen, S. J. Pol. Econ. 82 (1), 34–55 (1974) [Google Scholar]
- Oczkowski, E. Aus. J. of Agr. Econ. 38 (1), 93–110 (1994) [Google Scholar]
- Combris, P., Lange, C., & Issanchou, S. J. Wine Econ. 1 (1), 75–88 (2006) [CrossRef] [Google Scholar]
- Galletto, L., Rossetto, L. Wine Econ. and Pol. 4 (1), 60–68 (2015) [CrossRef] [Google Scholar]
- Landon, S., & Smith, C. E. J. of Cons. Pol. 20 (3), 289–323 (1997) [CrossRef] [Google Scholar]
- San Martín, G. J., Troncoso, J. L., & Brümmer, B. J. of Wine Econ. 3 (01), 72–84 (2008) [Google Scholar]
- Schamel, G. J. of Wine Econ. 4 (01), 62–80 (2009) [CrossRef] [Google Scholar]
- Schamel, G., & Anderson, K. Econ. Rec. 79 (246), 357–369 (2003) [Google Scholar]
- Lecocq, S., & Visser, M. J. of Wine Econ. 1 (02), 114–124 (2006) [CrossRef] [Google Scholar]
- Combris, P., Lecocq, S., & Visser, M. Appl. Econ. 32 (8) 961–967 (2000) [Google Scholar]
All Tables
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



