| Issue |
BIO Web Conf.
Volume 10, 2018
Contemporary Research Trends in Agricultural Engineering
|
|
|---|---|---|
| Article Number | 02005 | |
| Number of page(s) | 5 | |
| Section | Engineering and Technology | |
| DOI | https://doi.org/10.1051/bioconf/20181002005 | |
| Published online | 26 March 2018 | |
A Multistate Model of Reliability of Farming Machinery
1
Institute of Biosystems Engineering, Poznań University of Life Sciences, Poland
2
Department of Organisation and Production Engineering, Warsaw University of Life Sciences, Poland
* Corresponding author: karol.durczak@up.poznan.pl
The article describes a multistate model of reliability of farming machinery as a deductive stochastic model of the process of changes in the technical conditions observed during operation. These conditions determine the capacity of machinery to fulfil functions, simultaneously keeping safety and maintaining acceptable costs of possible repairs. The theory of semi-Markov processes was used to solve the problem. After detailed analysis of the symptoms of damage to exemplary groups of farming machinery (rotary mowers, rotary harrows and harvesting presses) we obligatorily and arbitrarily proposed an optimal four-state reliability model to describe changes in technical conditions. In contrast to the classic reliability theory, which allows only two states of technical usability (either a machine is fit to function or not), we also allowed intermediate states, because not all types of damage affect the functionality of machinery. This approach increases the probability of technical usability of machinery and rationally delays the moment of premature repair.
© The Authors, published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. (http://creativecommons.org/licenses/by/4.0/).
This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. (http://creativecommons.org/licenses/by/4.0/).
1 Introduction
Reliability is the ability of a technical device to perform its required functions under stated conditions for a specified time. According to the classic reliability theory, there are only two states of usability of a technical device, i.e. the state of being usable and the state of being unusable. A device is technically usable if it is able to perform its required functions at a specified moment or interval of time. The state of unusability is the opposite. The two-value approach to reliability, without intermediate states, simplifies reality, because there are repairable devices, composed of numerous parts, which form systems. Farming machinery is an example of such devices [1, 2, 3 and 4].
Contemporary machines, which are used at each farm, must be reliable due to the specific conditions of their work. Their periods of operation are usually long (ranging from a dozen years to several decades). They work together with other machines in simple or complex units (e.g. a tractor and plough unit, a sowing and cultivation unit) during short agrotechnical terms (ranging from a few hours while spraying orchards to a few weeks during harvesting) and under difficult field and weather conditions. Due to the specific character of their work an agrotechnical procedure can be conducted even if the machine is not fully technically usable. Therefore, the traditional reliability theory should be modified by introducing additional, acceptable states of reliability.
A four-state stochastic model was proposed to model the reliability of cars [5]. Apart from the state of full (complete) usability and the state of full (complete) unusability, the authors also assumed two intermediate states, i.e. the state of partial (incomplete) usability and the state of incomplete task-related usability. This approach seems to be justified and it can also be applied for the quantification of reliability of tractors and farming machinery. Hypothetically, there could be a different number of intermediate states between the state of usability and the state of unusability, so it requires an individual approach, depending on the group of machinery under consideration.
The aim of the study was to make methodological assumptions of a multistate probabilistic reliability model, which will allow for actual changes in the technical condition of farming machinery during field work. The theory of semi-Markov processes was used to solve the problem, as it is successfully used in many branches of business activity and fields of science [6, 7, 8, 9, 10, 11, 12, 13 and 14].
2 Material and methods
Many methods, which differ in precision and range of application, were developed to calculate indicators of the reliability of technical devices with a complex structure. There are analytical methods, simulations and mixed methods. Analytical methods of calculation enable detailed analysis of random events and processes. The Markov process method and, increasingly often, the semi- Markov process method are methods specialising in the analysis of random processes [15, 16, 17 and 18]. If the Markov process method is to be applied, we need an exponential distribution of the probability of damage, which causes some limitations. This distribution is characterised by constant intensity of damage λ = const. In practice, semi-Markov processes are proposed for the modelling of actual operation processes. They are characterised by the possibility to use various distributions of probability freely, which are generalisations of the exponential distribution, e.g. the Weibull distribution and the gamma distribution.
At the beginning it is necessary to make a very precise definition of complete usability of farming machinery. Only a brand-new machine which is released from a factory and has not worked even one hour (t = 0) is in the state of complete usability (CU) and its reliability amounts to R(0) = 1. As the machinery uptime increases, its reliability decreases. If the state of technical usability is not restored regularly, the state of complete unusability (CUn) will result. In practice, this situation should not occur and the state of usability should be restored regularly upon the observation of symptoms (organoleptic tests and diagnostic systems). A used machine will never achieve the 100% usability of a brand-new product. However, we made some simplifications of material reality in this study and the machine will achieve the CU state after being repaired.
According to the definition of reliability presented in the Introduction, a farming machine is in the state of usability only if is able to perform its required functions. The basic utility functions of farming machinery are listed in Polish standards – General Requirements and Tests, in the chapter: Operating Requirements. For example, the basic utility functions of tractor-drawn mouldboard ploughs are: stubble-field skimming and shallow pre-sowing ploughing on light and medium soils for skimming ploughs as well as medium and deep ploughing (pre-sowing and pre-winter ploughing) on all soil types for medium and deep ploughs (PN-89/R- 36598). These requirements are also specified for other groups of farming machinery, e.g. rotary mowers (PN- 90/R-36506). Their basic utility function is to mow meadow grass and low-stem green forage and to arrange it into windrows. A harvesting press is a tractor-drawn or self-propelled machine for collecting hay and straw in windrows or raked into rolls. Other utility functions are pressing (piston press) and baling (baler) (PN-91/R- 55026).
According to the Lorenz curve, even the simplest machines lose their properties during operation and pass into intermediate states (IN). If the symptoms indicating partial usability of a machine are ignored or overlooked, the usability of the whole machine may be reduced. In consequence, it may generate costs, which are particularly significant in the case of expensive farming machinery. Delays in sowing, spraying or harvesting due to an unexpected downtime and a major repair cause serious economic problems in agricultural enterprises.
The authors of this study proposed the graph method and the theory of semi-Markov processes to solve the problem of farming machinery passing from the CU through the IN to the CUn state.
The graph theory enables pictorial presentation of the functioning scheme of a particular process. Semi-Markov processes are stochastic processes with specific properties. In order to model the process of change in the technical condition of farming machinery and the states of its reliability the semi-Markov process {W(t): t ≥ 0} can be defined by means of the homogeneous Markov renewal process [19]. The process is fully defined if its function matrix is known:
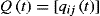 (1)
(1)This function matrix is an adjacency matrix whose elements are the probabilities of transition from state si to state sj over a period of time which is not longer than t (i ≠ j; i, j = 1, 2,…, k).
Another condition is to know the initial distribution of this process:
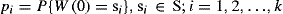 (2)
(2)The construction of the semi-Markov model {W(t): t ≥ 0} of the actual process of change in the technical condition of farming machinery as the states of its reliability is the sine qua non to apply the theory of semi- Markov processes. These models require that the following conditions be met:
the Markov condition, i.e. the future evolution of the state of any technical device must only depend on its present condition;
random variables: Ti (the duration of state si, no matter which state follows) and Tij (the duration of state si on condition that it is followed by state sj) must have non-exponential distributions.
3 Results
The operation of farming machinery under natural conditions enables distinction of a few characteristic changes in the technical condition. However, not all of these states make further effective and high quality operation of the machinery impossible. The long-term experience gained during research on operation let us observe several characteristic states of partial usability of farming machinery. Table 1 lists typical symptoms of the states of unusability of exemplary groups of farming machinery, which can be categorised as four universal classes.
Compiled by the authors
For further considerations concerning the reliability of farming machinery a set of four states was arbitrarily assumed S = {s1, s2, s3, s4}, as is shown in Figure 1.
The states are marked with nodes. The arcs with arrows show the relations, i.e. possible changes in the technical condition. Two values were allocated to the arcs, i.e. probability (p) and the time (T) of transition between individual states.
This arrangement comprises the use of a machine in state s1, when it is fully usable. When the machine is in the state of partial usability s2, it should be used until a certain agrotechnical process is finished and it should undergo renewal immediately afterwards. If it does not undergo renewal, it will pass into the state of incomplete task-related usability s3, which will increase costs and reduce safety and quality of work. When the machine is in this state, it should undergo renewal to state s1 with the least delay possible. States s2 and s3 should be as short as possible and the machine should undergo complete rather than partial renewal. Initial symptoms might signal a breakdown which will be expensive to repair. The transition from state s2 or s3 to state s1 does not require so much workload as the transition from state s4 to state s1. The final state s4 is the result of a random event known as total damage. A random breakdown event may cause this damage and disqualify the device from further use. The machine will lose its functionality.
All the states belonging to set S are values of a semi- Markov process. The elements of this set are consecutive states of reliability in a causal relationship‥ The transition graph showing changes in the technical condition of farming machinery during operation (Fig. 1) was used to make the following square function matrix:
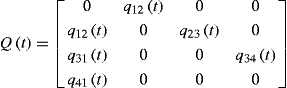 (3)
(3)According to the farming machinery operation schedule and the state of usability, a device can fulfil its tasks in two variants {W(t): t ≥ 0} [20]. These tasks must be performed while keeping adequate safety, efficiency and profitability, where the initial distribution {W(t): t ≥ 0} is written as follows [21]:
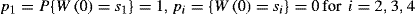 (4)
(4)The probabilities of change in states of reliability of farming machinery P = [pij; i,j = 1, 2, 3, 4] make the following transition probability matrix:
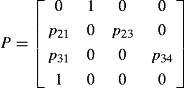 (5)
(5)As results from the matrix, only two transitions into states of the technical condition of farming machinery are certain in the process of their operation: transition from state s1 to s2 (p12 = 1) and the necessary transition from state s4 to s1 (p41 = 1) to make a repair.
In our example of the four-state model the limiting distribution πj (j = 1, 2, 3, 4) of the process {W(t): t ≥ 0} is determined by the following dependence [22]:
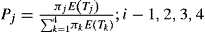 (6)
(6)where the limiting distribution is in accordance with the following equations:
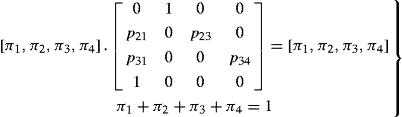 (7)
(7)When we solve the system of equations from the matrix (7) and use the theorem (6), we will receive the following equations:
P1=E(T1)M-1
P2=E(T2)M-1
P3=p23E(T3)M-1
P4=p23p34E(T4)M-1
for M = E(T1) + E(T2) + p23E(T3) + p23 p34E(T4)
where:
E(Tj) – the expected value of duration of state sj ∈ S(j = 1, 2, 3, 4); i.e. the average durability of a technical device pij – the probability of the process {W(t): t ≥ 0} transition from state si to state sj (si, sj ∈ S; i, j = 1, 2, 3, 4; i ≠ j) Pj – the probability of the process {W(t): t ≥ 0} remaining in state sj (j = 1, 2, 3, 4).
The variant of changes in the states of reliability discussed in this article presents the situations in which the user may deliberately take the risk to continue work, remembering that it will reduce its quality and safety and it will involve higher costs. As results from experience, it is recommended to operate farming machinery in the state of complete usability s1 and possibly in the state of partial usability s2, having made a deliberate decision to do so. The reliability of this system increases to the value P1+P2. States s3 and s4 should be treated as states of damaged machinery, which make further operation impossible.
The states of reliability of selected groups of farming machinery and possible symptoms of damage
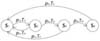 |
Fig. 1. A directed graph of the four-state model of the actual process of farming machinery operation. |
4 Conclusion
We used the system method of constructing deductive models and the theory of semi-Markov processes to make a four-state model of reliability of farming machinery. The process is continuous in time and discreet in states. The mathematical and logical analysis of the process as well as the examples given in the study led to the following conclusions:
- 1.
The four-state model of reliability correctly describes the processes occurring during the operation of farming machinery. It presents the actual changes in the technical condition better than the classic reliability theory.
- 2.
The model allows for the state of partial technical usability of machinery (state s2). Under normal conditions of use there is damage which does not influence effective operation of the machinery.
- 3.
When we know intermediate states, in theory it is possible to restore complete usability of machinery repeatedly until it is morally obsolete. Therefore, the indicators of costs of repair of farming machinery might be as high as 100-150% of its price [23].
- 4.
The multistate approach is a reliable reflection of the material reality. The article provides the method which can be adapted and used according to one’s heuristic knowledge by making individual adjustments concerning intermediate states and the probable consequences of ignoring them. It is the user that makes an arbitrary decision about the acceptable quality of work, safety and costs of repair of machinery.
References
- W. Adamkiewicz i in., Badania i ocena niezawodności maszyn w systemie transportowym. (Wydawnictwa Komunikacji i Łączności, 1983) [Google Scholar]
- L. Dwaliński, Niezawodność maszyn rolniczych. (Wema, 1988) [Google Scholar]
- T. Otmianowski, Procesy odnowy maszyn i ciągników rolniczych. (Państwowe Wydawnictwo Rolnicze i Leśne, 1983) [Google Scholar]
- C. Rzeźnik, Podstawy obsługi technicznej maszyn rolniczych. (Wydawnictwo Akademii Rolniczej w Poznaniu, 2008) [Google Scholar]
- J. Girtler, M. Ślęzak, Eksploatacja i Niezawodność – Maintenance and reliability 15 (2), 156–160 (2013) [Google Scholar]
- J. Paska, Niezawodność systemów elektroenergetycznych. (Oficyna Wydawnicza PW, 2005) [Google Scholar]
- S. McClean, A. Papadopoulou, G. Tsaklidis, Communication in Statistics – Theory and Methods 33 (6), 623-638 (2004) [CrossRef] [Google Scholar]
- M. Matalytski, O. Tikhonenko, Procesy stochastyczne. (Akademicka Oficyna Wydawnicza EXIT, 2011) [Google Scholar]
- R. Magiera, Statystyczne funkcje decyzyjne, (Oficyna Wydawnicza GiS 2016) [Google Scholar]
- M. Sobczyk, Statystyka, (Wydawnictwo Naukowe PWN 2017) [Google Scholar]
- J. Jiang, G. G. Roussas, F. J. Samaniego, Nonparametric Statistical Methods and Related Topics, (World Scientific Publishing Company, 2012) [Google Scholar]
- D. J. Smith, Reliability maintainability and risk. Practical Methods for Engineers, (ButterworthHeinemann, 2011) [Google Scholar]
- E. Zio, Introduction to the Basics of Reliability and Risk Analysis, (World Scientific Publishing Company, 2007) [CrossRef] [Google Scholar]
- S. Keller-McNulty, Modern Statistical And Mathematical Methods in Reliability, (World Scientific Publishing Company, 2005) [Google Scholar]
- P. Lev’y, Proceesus semi-markoviens. (Proc. Int. Cong. Math, Amsterdam, 416–426, 1954) [Google Scholar]
- R. Pyke, Ann. of Math. Statist., 32, 1243–1259 (1961) [Google Scholar]
- R. Pyke, R. Schaufele, Ann. of Math. Statist., 32, 1746–1764 (1964) [CrossRef] [Google Scholar]
- M. Rosenblatt, Procesy stochastyczne. (PWN, 1967) [Google Scholar]
- J. Girtler, Zagadnienia Eksploatacji Maszyn 3,419-428 (1996) [Google Scholar]
- F. Grabski, Teoria semi-markowskich procesów eksploatacji obiektów technicznych, (AMW, 1982) [Google Scholar]
- J. Girtler, The Archives of Automotive Engineering (Archiwum Motoryzacji) 3,165-196 (2004) [Google Scholar]
- F. Grabski, Semi-markowskie modele niezawodności i eksploatacji. (IBSPAN, 2002) [Google Scholar]
- A. Muzalewski, Koszty eksploatacji maszyn. (Wyd. IBMER, 2006) [Google Scholar]
All Tables
The states of reliability of selected groups of farming machinery and possible symptoms of damage
All Figures
 |
Fig. 1. A directed graph of the four-state model of the actual process of farming machinery operation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



