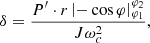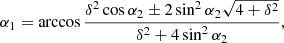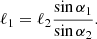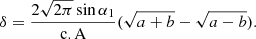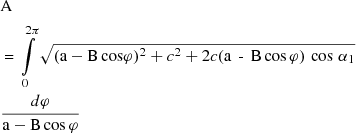| Issue |
BIO Web Conf.
Volume 17, 2020
International Scientific-Practical Conference “Agriculture and Food Security: Technology, Innovation, Markets, Human Resources” (FIES 2019)
|
|
|---|---|---|
| Article Number | 00012 | |
| Number of page(s) | 5 | |
| DOI | https://doi.org/10.1051/bioconf/20201700012 | |
| Published online | 28 February 2020 | |
Study of spatial hinge mechanisms and their use in agricultural machines
1
Kazan State Agrarian University, 420015 Kazan, Russia
2
Kazan State University of Architecture and Civil Engineering, 420043 Kazan, Russia
* Corresponding author: mudrov.aleks@yandex.ru
The article studies spatial mechanisms with rotational kinematic pairs (hinges) whose geometric axes are crossed at different angles and dependent on the shortest distances between these axes which are the theoretical lengths of the links. There is little information about their use in agricultural machines. There is no open information about the technology used for manufacturing models and field samples. The study describes applications of these mechanisms in agricultural machinery.
© The Authors, published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Spatial mechanisms used in machines can be divided into two groups: mechanisms with kinematic spherical pairs, spherical pairs with a finger, ball-tube pairs, cylindrical pairs and rotational pairs (hinges).
The first group has been well studied; these mechanisms can be easily produced [1–4]. As for the spatial mechanisms with rotary joints, it is difficult to design them, since there was a significant gap between theory and practice [5–8]. One of the first mechanisms of this group was the Cardan-Hook spherical mechanism widely used to transmit motion. The researchers tried to create other mechanisms with rotary joints. There was no such system and theory of production of such mechanisms; they were created by a combination of links by trial and error. However, the links did not rotate, and the mechanisms were inoperative.
In 1903, the English mathematician Bennett published articles on a four-link mechanism with cylindrical joints (the Bennett mechanism), whose axes are neither parallel nor intersect (cross) [9]. Later, Russian and foreign scientists began to study this mechanism. For this group of mechanisms, it is necessary to observe angular and linear parameters of the links and their interconnection, otherwise the mechanism will be inoperative. Identification of these parameters (angles and shortest distances) is one of the difficulties in designing such mechanisms.
Researchers wrongfully believed that the lengths of adjacent links intersected at one point. The researchers could not find a way to eliminate this paradoxical discrepancy between the theoretical and actual lengths of the links; therefore, they could not create a working model.
Only 75 years after Benett published his article, Kazan scientists B.V. Shitikov [10] and P.G. Mudrov [11] managed to solve this problem. A four-link mechanism model was produced, and a theory of production of other mechanisms (five, six, seven-link, multi-link mechanisms and differential mechanisms) was developed.
Since the four-link mechanism was theoretically discovered by Bennett in 1903, the model developed by B.V. Shitikov was called “Bennett-Shitikov mechanism”. The first scientist discovered it theoretically, and the second one made and applied it in practice, developed a new scientific direction in the science of spatial mechanisms with rotational hinges.
2 Materials and methods
Spatial mechanisms with rotary joints are used in agricultural machines.
1. Drives of agricultural machines (8 inventions) for transmitting motion between crossing shafts: a drive of the high-speed cutting tool, a drive of the belt of a conveyor of the potato harvester, a drive of the disc drive of the beet harvester, etc. The mechanisms simplify the tools and increase their reliability and durability. Figure 1 shows the drive circuit of a high-speed cutting tool with a spatial four-link Bennett-Shitikov mechanism [12].
The device includes a knife strip with segments con-nected with three cranks of radius r, frame 4 and the Bennett-Shitikov mechanism consisting of leading crank 1, driven crank 3 and connecting rod 2. Driven crank 3 is connected to the third extended crank of the cutting de-vice at an angle β equal to 210-2200. Since stems are cut in the first half of knife strip revolution, the second half is idle; as a result, the strip with segments has an uneven movement; the inertial moment negatively affects the structure.
To eliminate this point, the coefficient of unevenness δ of the movement of the knife strip is determined:
where P′- stalk cutting force; r – crank radius; φ1 and φ2 – angles of rotation of the cranks of the cutter at which Mp=0 (their value φ1=arc∙sin 1/π, φ2=180°-φ1); J – total moment of inertia of the rotating links; ωc – average value of angular speed of the cranks.
Then, using a coefficient of unevenness, the spatial mechanism is designed; in particular, angle α1 at which the hinge axes cross is determined by formula (2)
where δ – the degree of uneven rotation of the cranks of the cutter with a knife strip; α2 – the angle of intersec-tion of the axes of hinges of the mechanism (set based on design considerations, as well as the shortest distance ℓ2)
To determine the shortest distance ℓ1 the following expression is used [9],
Thus, expressions (2) and (3) determine the parameters of the cranks with required properties to equalize the angular velocity and reduce the inertial moment.
In order to reduce (eliminate) the oscillations of the frame resulting from uneven rotation of the cranks, it is to to attach the leading crank to driven crank 3 of the Bennett-Shitikov mechanism so that the geometric axes of their lengths are located at angle p equal to 210-2200.
The second application of the spatial five-link mechanism is presented in Figure 2. It is a device for a bar conveyor that increases soil separation and reduces trauma to potato tubers [13]. The device includes two spatial cranks and two connecting rods. Figure 2a shows two connecting rods and interchangeable crank spikes; Figure 2b shows a potato digger containing this mechanism.
An increase in soil separation is achieved due to the fact that the soil layer has relative motion in the impact zone of the shakers and along the entire length of the canvas. This occurs under the influence of the uneven motion of the canvas with variable force Q acting on the soil layer. The larger the amplitude of the oscillations of this force, the greater the deformation of the layer which destroys and intensifies its separation. It is confirmed by the calculation results presented (see Figure 3) by the graphs of the dependence on rotation angle 91 of the driving crank of the elevator drive: QX – along the surface of the canvas and QY – perpendicular to it.
The graphs show that variable loads act on the soil and potato layer, it “vibrates” being fixed to the elevator bed. In addition, with such a potato digger drive, the shaker sprockets and a vibration grate are no longer needed, which simplifies the design and reduces the potato digger metal consumption
2. Devices for primary processing (14 inventions). Spatial link mechanisms are used to convert the constant angular velocity of the driving crank into the variable velocity of the driven crank. This property is used to ensure non-stationary operation of many devices in order to intensify the process of mixing components in drum mixers. In these devices, the connecting rod is a carrier of the working bodies: spatial mixers, tilters for polishing and grinding parts, hardening products, seed dressing, etc. [12].
Figure 4 shows a spatial inertial mixer containing the Bennett-Shitikov mechanism whose tank is fixed on a connecting rod. When the mixer is operating, the leading crank rotates at a constant angular velocity, and the follower rotates with a variable velocity, while the planes of crank rotation are in perpendicular planes, the container will make a complex spatial movement with a controlled inertial effect on the material being processed. As a result, the intensification of processing increases several times in comparison and processing quality is maximum.
Another type of a mixer containing the Bennett-Shitikov mechanism is shown in Figure 5 [14]. In this mixer, the container (drum) makes two turns in one revolution of the leading crank, i.e. the mixer can reduce motion.
The tank has a spiral spatial non-uniform motion with a controlled inertial effect on the processed materi-al. Figure 6 shows a complex movement of the vertical axis PP ′ of the mixer drum (Figure 7).
In addition, the mixer drum moves at a variable angular speed ωб, determined as 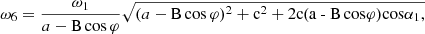
where a=1−cosα1cosα2, ѵ=sinα1sinsinα2, c=cosα2−cosα1, φ – turn angle and ω1 – angular speed of the input crank, α1, α2 – the angles of intersection of axes of the hinges of the cranks and drum, respectively. Variability of the angular speed of the drum is characterized by the same coefficient of unevenness δ:
Here
The variability ensures a high efficiency of the mix-ing process in a spatial screw mixer.
3. Devices for washing and cleaning products (8 inventions). This group includes devices for washing vehicles, cleaning hollow products, watch mechanisms. One of the structures for cleaning large-sized products is transmission housings of the DT-54 tractors shown in Figure 8. The Bennett-Shitikov mechanism is used as a base [15, 16]. The study of washing machines based on spatial mechanisms with rotary hinges have confirmed their performance. The same is true for devices with a stirrer whose rotor blades rotate with an in-cycle change in angular velocity, as a result of which the fluid movement is activated throughout the volume, and the mixture formation is accelerated with an increase in the degree of homogeneity of the composition. The movement can be carried out by four-link, five-link and six-link mechanisms.
4. Inertial devices (5 inventions): an inertial engine, a vibro-loader for immersing and pulling pipes, piles, etc., a device for tamping soil, silage, etc.
Figures 9 and 10 show a spatial vibration absorber and its kinematic scheme. Each of the mechanisms of the drive of debalances 9 and 10 of the vibration damper (see Figure 9) is an example of the Bennett-Shitikov mechanism.
The rotation of the shaft of electric motor 2 is converted into a synchronous rotation of the debalances in opposite directions at a variable angular speed per revolution. Due to the uneven rotation of the debalances, the driving force of the vibrator changes which creates a power pulse sufficient to immerse or pull out the pipe.
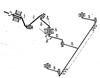 |
Fig. 1. The diagram of the cutter |
 |
Fig. 2. Potato digger conveyor drive: a) interchangeable cranks and two connecting rods b) a drive |
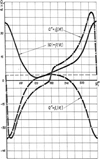 |
Fig. 3. Graphs of the soil pressure on the layer |
 |
Fig. 4. The inertial mixer |
 |
Fig. 5. The screw mixer |
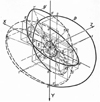 |
Fig. 6. Trajectories of the drum points |
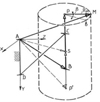 |
Fig. 7. The kinematic diagram of the screw mixer |
 |
Fig. 8. Washer |
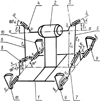 |
Fig. 9. The kinematic diagram of the vibration driver |
 |
Fig. 10. The spatial vibration driver |
3 Results and discussion
The study of spatial mechanisms with rotational pairs is carried out by the TMM department of Kazan Agrarian University under the guidance of Professor P.G. Mudrov. Unfortunately, Russian and foreign scientists have not dealt with practical aspects.
Some of the devices have already been introduced into agricultural production processes: spatial mixers, tools for seed grinding, mechanisms for driving a potato digger elevator, etc.
Devices containing spatial linkage mechanisms with rotational pairs were awarded with two silver and two bronze medals of the Exhibition of Economic Achievements of the USSR, NTO prizes of agriculture, and the III-degree diploma of the Ministry of Higher and Secondary Education of the Russian Federation.
4 Conclusion
The article described some agricultural machines containing spatial hinge-link Bennett-Shitikov mechanisms. The mathematical models of kinematics and dynamics make it possible to intensify the process of producing these devices and increase their quality and efficiency; rotational pairs in the form of hinge assemblies protected from the external environment can improve their reliability.
References
- N. I. Mertsalov, Theory of spatial mechanisms (Mashgiz, Moscow, 1951) [Google Scholar]
- V.P. Goryachkin, Collected works. Vol. 2. Earth mechanics (Selkhozgiz, Moscow, 1937) [Google Scholar]
- E.I. Vorobyov, F.M. Dimenberg, Spatial joint mechanisms. Closed and open kinematic chains (Nauka, Moscow, 1991) [Google Scholar]
- A.V. Verkhovskiy, Six-dimensional spatial articulated mechanisms Bulletin of Tomsk Technological Institute 61(1), 47–52 (1947) [Google Scholar]
- V.A. Zinovyev, Spatial mechanisms with lower pairs (Gostekhizdat, Moscow, 1952) [Google Scholar]
- A.N. Evgrafov, G.N. Petrov, Calculation of geometric and kinematic parameters of the spatial link mechanism with excessive links Problems of mechanical engineering and machine reliability 3, 3–8 (2013) [Google Scholar]
- F.M. Dimenberg, Theory of spatial articulated mechanisms (Nauka, Moscow, 1982) [Google Scholar]
- V.A. Glazunov, A. Sh. Koliscor, A. F. Krainev, Spatial mechanisms of parallel structure (Nauka, Moscow, 1991) [Google Scholar]
- G.T. Bennett, A new mechanism Engineering 76, 777–778 (1903) [Google Scholar]
- B.V. Shitikov, The study of spatial articulated mechanisms. Research report (KHTI, Kazan, 1958) [Google Scholar]
- P.G. Mudrov, Spatial mechanisms with rotational pairs (Kazan University, Kazan, 1976) [Google Scholar]
- A.G. Mudrov, Spatial mechanisms with a special structure (School, Kazan, 2003) [Google Scholar]
- Sh. R. Galiullin, Justification of the parameters of a bar elevator with uneven movement of the blade to increase a separating ability of the potato harvester: Thesis (VIM, Moscow, 1989) [Google Scholar]
- A.P. Mudrov, Theoretical foundations of the analysis and design of a spatial screw mixer. Thesis (HTI, Kazan, 1989) [Google Scholar]
- M.G. Yarullin, Intensification of cleaning products in submersible washing machines based on spatial mechanisms: Thesis (MGAU, Moscow, 2002) [Google Scholar]
- M.G. Yarullin, Three-dimensional hydrodynamic cleaning of products (Kazan University, Kazan, 2001) [Google Scholar]
All Figures
 |
Fig. 1. The diagram of the cutter |
| In the text | |
 |
Fig. 2. Potato digger conveyor drive: a) interchangeable cranks and two connecting rods b) a drive |
| In the text | |
 |
Fig. 3. Graphs of the soil pressure on the layer |
| In the text | |
 |
Fig. 4. The inertial mixer |
| In the text | |
 |
Fig. 5. The screw mixer |
| In the text | |
 |
Fig. 6. Trajectories of the drum points |
| In the text | |
 |
Fig. 7. The kinematic diagram of the screw mixer |
| In the text | |
 |
Fig. 8. Washer |
| In the text | |
 |
Fig. 9. The kinematic diagram of the vibration driver |
| In the text | |
 |
Fig. 10. The spatial vibration driver |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.