| Issue |
BIO Web Conf.
Volume 17, 2020
International Scientific-Practical Conference “Agriculture and Food Security: Technology, Innovation, Markets, Human Resources” (FIES 2019)
|
|
|---|---|---|
| Article Number | 00058 | |
| Number of page(s) | 4 | |
| DOI | https://doi.org/10.1051/bioconf/20201700058 | |
| Published online | 28 February 2020 | |
Research of transportation of hard-running seeds with a torsion-pin sowing machine
Samara State Agrarian University, 446442 Kinel, Samara region, Russia
* Corresponding author: kotov_d@bk.ru
The article describes patterns of transportation of hard-running seeds by working bodies of the torsion-pin sowing machine. An analytical expression for determining the volumetric supply of hardrunning seeds by working bodies of the torsion-pin sowing unit at the stage of their transportation is substantiated. Graphical dependences of the volumetric feed on the number and height of vertical pins are provided.
© The Authors, published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Various soil and climatic conditions have a significant impact on the productivity and successful seed production of legumes. Moreover, they are not always favorable for their highly productive cultivation, since for germination of legume seeds, an increased amount of moisture is required [1, 2].
Therefore, for regions with insufficient moisture in the spring, including Samara region, in order to increase field germination and have high yields, a technology for sowing legumes with soaked seeds was developed [3].
However, in soaking, legume seeds become cohesive, hard-running.
The problem of sowing hard-running sowing materials cannot be solved using existing sowing machines [4–8], since when dosing seeds that have undergone soaking treatment, arches above the hopper outlet [9, 10], as well as sticking of seeds to the working bodies of the dosing device may occur [11].
2 Materials and methods
To solve the problem of sowing hard-running seeds that have undergone pre-sowing treatment by soaking, a torsion-pin sowing machine was designed. Its technological process (Fig. 1) is as follows.
During the expiration from the hopper, the seeds fill the space between torsion-pin groups 6 mounted on drive shaft 1 and consisting of a horizontal pin, a torsion spring and vertical pins 7. When drive shaft 1 is rotated, the seeds move torsion-pin group 6 to upper segment (peak) 3.
Vertical pins 7, abutting against visor 3, deflect under the action of the spring, and the compacted mass of seeds moves to sowing slit 5, falling into the funnel of the seed drop tube.
The destruction of the arches that impede the movement of hard-running seeds through the outlet window of the hopper is carried out due to the impact of vertical pins 7, when seeds are returned to their upper position by a torsion spring.
The size and stability of the feed is determined by the transporting ability or the ability to move the increased volume of seeds by torsion-pin groups 6 with vertical pins 7, at the stage of their transportation to upper segment (peak) 3.
Proceeding from the technological process of transportation of hard-running seeds by the working bodies of the torsion-pin sowing machine, the torsion-pin group forms a movable seed volume, consisting of the seed volume moved by horizontal pin 1 and the seed volume moved by vertical pins 2 (Fig. 2).
The volumetric supply of seeds Q (m3/s) by a torsion-pin group with vertical pins can be determined by the following expression: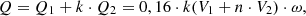 (1)
(1)
where Q1 is the volumetric feed of seeds formed by the horizontal pin of the torsion-pin group, m3/s; Q2 -volumetric feed formed by vertical pins, m3/s; k – the number of torsion-pin groups, pcs .; V1 – the volume of seeds formed by one horizontal pin, m3; V2 is the volume of seeds formed by one vertical pin, m3; – the number of vertical pins, pcs .; ω- the angular velocity of rotation of the shaft of the metering unit, s−1.
The seed volume V1 formed by one horizontal pin of the torsion-pin group during rotational movement is a volumetric figure with an OABC section (Fig. 2) with an angle at the base ψ equal to the dynamic angle of internal friction of the seed material.
The volume V1 formed by one horizontal pin is determined by the expression (2)
(2)
where μ is the empirical coefficient that takes into account features of transportation of hard-running seeds; h1 – the height of the torsion-pin group, m; δ – the diameter of the horizontal pin of the torsion-pin group, m; D – the outer diameter of the sector of seed collection, m; d – the inner diameter of the sector of the seed collection, m
The additional volume of seeds transported by one vertical pin is formed in the form of figure F (DCDEF), part of which is cut off by upper sector 3 (Fig. 2).
To calculate volume V2, let us single out a small element with height dh. The volume of the element is determined by formula: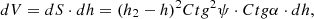 (3)
(3)
where dh is the height of the selected element, m; dS is the area of the selected element, m2; α is the angle of a dynamic slope formed during the expiration of the seed between the vertical pins, degrees.
After integrating expression (3), volume V2 formed by one pin is determined by equation: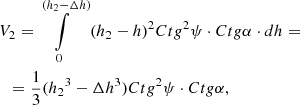 (4)
(4)
where Δh = (h1 +δ+ h2) - h is the height of the figure Φ (DCDEF), cut off by the upper sector (visor), m; h3- the height of the upper sector (peak), m.
The volumetric seed supply Q formed by the torsion-pin groups, taking into account expression (1), can be written as: (5)
(5)
As can be seen from expression (5), volumetric supply Q depends on structural and technological parameters and physicomechanical properties of seeds.
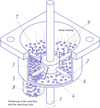 |
Fig. 1. Diagram of the technological process of the torsion-pin sowing machine: 1 – drive shaft, 2 – metering body, 3 – upper segment (visor), 5 – metering slot, 6 – torsion-pin group (TPG) with vertical pins 7, 8 – seed tube, 9 – seeds. |
 |
Fig. 2. Scheme for determining the volume of a figure formed by one horizontal pin (on the right) and a vertical pin, torsion-pin group (on the left). |
 |
Fig. 3. Theoretical Qteor and experimental Qexp dependences of the volumetric feed on the number of vertical pins n and the height of the vertical pins h2. |
3 Results
Let us substitute structural and technological parameters of the torsion-pin sowing machine in expression (5): the number of torsion-pin groups k = 4; the number of pins n = 2, 3, 4; the height of the torsion-pin groups h1 = 9 mm; the height of the vertical pins h2 = 5, 10, 15, 20 mm; the diameter of the horizontal pin d = 8 mm; the height of the upper sector (visor) h3 = 18 mm; the external diameter of the sowing machine D = 132 mm; the outer diameter of the sleeve d = 64 mm; the angular velocity of the shaft m = 1,57 s-1.
We used soaked seeds of white annual melilot, whose physical and mechanical properties changed and amounted to: the coefficient of internal friction f = 0.8; flow coefficient y = 0.5; caving angle a = 55 °.
In accordance with the physical and mechanical properties of the soaked seeds of white annual melilot, the empirical coefficient was determined taking into account peculiarities of transportation of hard-running seeds. It is = 1.31.
The calculation results are presented in the form of graphical dependences of volumetric feed Qteor on the quantity n and the height of the vertical pins h2.
To compare the convergence of the theoretical data, the graphical dependences Qexp are plotted based on the results of experimental studies (Fig. 3).
From the analysis of graphical dependences, there is a high convergence of the results of theoretical and experimental research data when 4 vertical pins are installed at their height up to h2 = 15 mm, estimated by a correlation coefficient of 98%.
When installing two vertical pins, a high convergence of the results up to h2 = 10 mm is observed; it is estimated by a correlation coefficient of 95%.
With an increase in the height of the vertical pins, the convergence of the results of theoretical calculations with the data of experimental studies decreases due to the fact that when the height of the vertical pin h2 = 20 mm and higher, the sowing process is implemented with non-optimal quality parameters.
Therefore, to optimize the design parameters of the torsion-pin sowing device, it is necessary to increase the height of the vertical pins up to h2 = 20 mm.
4 Conclusion
The analytical expression (5) allows us to determine the volumetric supply of hard-running seeds by torsion-pin groups at the stage of their transportation by a torsion-pin sowing machine. In this case, the volumetric feed depends on the structural and technological parameters of the torsion-pin sowing machine and the physical and mechanical properties of the seeds. The adequacy of the mathematical model is confirmed by the data of experimental studies.
References
- V. F. Kazarin, A.V. Kazarina, L.K. Marunova et al., Resource-saving technology for cultivation of white melilot in the forest-steppe of the Middle Volga (Kinel, 2014) [Google Scholar]
- G. A. Medvedev, Perennial grasses under irrigation Retrieved from: http://agrolib.ru/books/item/f00/s00/z0000043/st004.shtml. [Google Scholar]
- N.P. Kryuchin, A.M. Petrov, O.A. Artamonova, Development of technology for pre-sowing preparation of legume seeds Bulletin of the Orenburg State Agrarian University 5, 99–102 (2018) [Google Scholar]
- A. M. Petrov, Substantiation of seeding technology and parameters of a pin sowing device of a pneumatic seeder for sowing soaked seeds of Eastern goatskin, candidate dissertation (Saratov, 1994) illustrations [Google Scholar]
- S.V. Vdovkin, P. V. Kryuchin, Yu. M. Isaev, N. M. Semashkin, Theoretical substantiation of the technological process of universal disk-brush sowing machine Proc. of the Samara state agricultural Academy 3, 22–28 (2014) [Google Scholar]
- P. Balsari, M. Manzone, P. Marucco, M. Tamagnone, Evaluation of seed dressing dust dispersion from maize sowing machines Crop Protection 51, 19–23 (September 2013) [CrossRef] [Google Scholar]
- A.M. Petrov, V.A. Syrkin, The results of field studies of the experimental selecton seeder with a coil-pin seeding machine Proc. of the Samara state agricultural Academy 2, 36–39 (2017) [CrossRef] [Google Scholar]
- N.I. Seomushkin, B.G. Ziganshin, S.M. Yakhin, B.A. Gayfullin, R.E. Vlasov, Mathematical model of interaction of seeds with the internal surface of sowing block of seed drill J. of Research in Science Teaching 531, 531 (2012) [Google Scholar]
- Yu. M. Isaev, N. M. Semashkin, Spiral-Screwing Device for Graining of Grain Material Int. J. of Mechanical Engineering and Technology 9(2), 622–628 (2018) Retrieved from: http://www.iaeme.com/IJMET/issues.asp?JType=IJMET&VType=9&IType =2. [Google Scholar]
- O.N. Kukharev, N.P. Larushin, A device for guiding of bodies of irregular shape Research J. of Pharmaceutical, Biological and Chemical Sciences 9(3), 30–33 (2018) [Google Scholar]
- Yu. M. Isaev, N.P. Kryuchin, N.M. Semashkin, A.N. Kryuchin, Theoretical studies of movement of loose material in a dosing device Int. J. of Mechanical Engineering and Technology (IJMET) 9(5), 834–840 (May 2018) Article ID: IJMET_09_05_092 Retrieved from: http://www.iaeme.com/ijmet/issues.asp?JType=IJMET&VType=9&IType=5. [Google Scholar]
All Figures
 |
Fig. 1. Diagram of the technological process of the torsion-pin sowing machine: 1 – drive shaft, 2 – metering body, 3 – upper segment (visor), 5 – metering slot, 6 – torsion-pin group (TPG) with vertical pins 7, 8 – seed tube, 9 – seeds. |
| In the text | |
 |
Fig. 2. Scheme for determining the volume of a figure formed by one horizontal pin (on the right) and a vertical pin, torsion-pin group (on the left). |
| In the text | |
 |
Fig. 3. Theoretical Qteor and experimental Qexp dependences of the volumetric feed on the number of vertical pins n and the height of the vertical pins h2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



