| Issue |
BIO Web Conf.
Volume 27, 2020
International Scientific-Practical Conference “Agriculture and Food Security: Technology, Innovation, Markets, Human Resources” (FIES 2020)
|
|
|---|---|---|
| Article Number | 00120 | |
| Number of page(s) | 6 | |
| DOI | https://doi.org/10.1051/bioconf/20202700120 | |
| Published online | 25 November 2020 | |
Calculation of making doses of fertilizers under planned yield of spring wheat using an artificial neural network
1
Kazan State Agrarian University, Kazan 420015, Russia
2
Kazan National Research Technical University named after A.N. Tupolev-KAI, Kazan 420015, Russia
* Corresponding author: samadvaliev@rambler.ru
This paper is devoted to the study of the construction and application of an artificial neural network for calculating the doses of fertilizer application at the planned yield level in the conditions of grey forest soils of the Republic of Tatarstan. When using mineral fertilizers for crops, it is crucial to comply with the norms and doses of the introduced substances. An overabundance of fertilizer leads to residual accumulation in the soil. Lack of quantity of applied doses affects the quality of the crop, as well as the fertility and ecological situation of agricultural lands. High modern technology and information tools allow solving this problem.
© The Authors, published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Improvement of the quality and productivity of spring wheat is one of the main tasks of the agro-industrial complex of the Russian Federation at present. Spring wheat crop formation is a complex process of influence of many factors that have a complex interaction structure. Influencing factors on wheat productivity can be divided into two groups.
The first group is uncontrollable factors associated with natural and climatic conditions. The second group is regulated factors responsible for the provision of soils with NPK and microelements. Providing soils with mineral fertilizers and microelements for cultivating wheat implies the maximum supply of plants with nutrients, as well as changing the properties of soils, increasing its fertility and the interconnection of all processes in the ecosystem.
At the present stage of development of our society in almost all sectors and spheres of the national economy, artificial neural networks have been widely used for solving various problems. Neural network models allow an intelligent analysis of multidimensional data, taking into account all the complex relationships between influencing factors, and at the same time solve the forecasting problem.
The use of the neural network model allows targeted control of regulated factors with average values of uncontrollable factors, which allows increasing productivity [1–3]. For increasing the economic development of the economy, it is necessary to make optimal decisions in time to ensure soil fertility by applying NPK and microelements to the soil [4-11].
2 Conditions, research methods
For solving the studied problem, it is necessary to build a nonlinear model capable of calculating the amount of NPK fertilizer application for a given yield. The condition for building the model is to take into account all the influencing factors.
The search for the optimal values of the factors affecting the yield of spring wheat is possible in the presence of a regression equation in the form of a polynomial of the second degree. However, in the available analytical packages, the construction of a nonlinear regression model is possible only with a small number of factors. Therefore, in this work, an artificial neural network was used for planning the yield of spring wheat.
Neural network models are often used in various fields of research. The tasks of forecasting, nonlinear regression, systems of equations are solved using neural models. Neural networks can generalize data, learn from their own mistakes, select the answer “by analogy.” In our work, the neural network model was used as a nonlinear regression for calculating the doses of fertilizer for spring wheat.
3 Results
The novelty of the presented study is the development of a neural network model that will allow calculating the doses of mineral fertilizers for the planned yield levels of spring wheat in the grey forest soils of the Republic of Tatarstan.
The studied sample of experimental data for 37 years, consisting of eighteen influencing factors on the yield and average yield of spring wheat:
the amount of fertilizers NO3, P2O5 and K2O;
productive moisture on the day of sowing,
the sum of the effective temperatures during the growing season, the temperature in May and June, the temperature in June,
air humidity,
precipitation during the growing season, precipitation in May and June, precipitation in June,
growing season,
grain weight per spike,
weight of 1000 grains
gluten mass fraction,
content of easily hydrolyzable nitrogen in the soil,
the content of P2O5 in the soil,
K2O content in the soil.
Table 1 presents a fragment of this sample.
Kolmogorov’s theorem on the sufficient structure of a neural network was used for selecting the architecture of the neural network, in particular, the number of hidden layers, the number of neurons in each of them, and the activation functions of neurons. According to Kolmogorov’s theorem, to transform an N-dimensional input vector of a set of input data x into an M-dimensional output vector d, it is sufficient to use a neural network with one hidden layer. With N input neurons, to implement the approximating function, it is sufficient to use (2N + 1) neurons in the hidden layer.
As a result, a three-layer neural network model was constructed with one hidden, one input, and one output layer.
For selecting the number of neurons in the inner layer of the neural network model, 14 models with different numbers of neurons were constructed according to the network extension method [12]. The number of hidden layer neurons varied from 2 to 15. When testing these models, calculation errors were obtained and analyzed on the test data set, which is presented in Table 2. According to the results (Table 2), it is seen that the model with four neurons in the hidden layer is the most effective model.
Hyperbolic tangent as a nonlinear transducer providing a neural network model of the properties of a universal approximator was chosen as the activation function of hidden layer neurons.
The number of training epochs was selected experimentally according to the following methodology: at each epoch of training, two error values were tracked, namely, on the training and test sets. On the training set, the error value monotonously decreases. In contrast, on the test set, after the error decreases with a further increase in the number of epochs, the error begins to increase. This process corresponds to the so-called “retraining” of the neural network. The optimal number of eras for learning, therefore, is that at which the test error reaches its minimum.
As a result of a series of experiments, the number of 1000 epochs for training the network was selected. In particular, it is recommended to choose a three-layer perceptron with a linear function for activating the output layer and hyperbolic tangent for the hidden layer. The response of the neural network, in this case, can be represented as:
Here N is the dimension of the input vector; S is the number of neurons in the hidden layer; M is the number of neurons in the output layer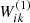 ; - weighting coefficients of the hidden (first) layer
; - weighting coefficients of the hidden (first) layer  , defined at the training stage;
, defined at the training stage;  - weighting factors of the output layer
- weighting factors of the output layer 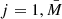 determined at the training kj stage. Figure 1 shows this diagram.
determined at the training kj stage. Figure 1 shows this diagram.
The constructed three-layer neural network has 16 neurons in the input layer, four neurons in the inner layer and three neurons in the output layer. The graph of the constructed neural network is shown in Figure 1. The input data are the yield of the studied culture and the last 15 factors from Table 1. As the neurons in the output layer, the amount of fertilizer applied was selected.
The neural network was trained and tested on a set of initial data from Table 1, which were previously randomly divided into two sets: training (95% of data tuples) and test (5% of data tuples). An online learning algorithm was used. The correction of the weights was made after the presentation of each example of the learning set. The condition for the termination of training was the value of the learning error less than 0.005, or the achievement of a given era (1000). Figure 2 presents this diagram.
The trained neural network was used for calculating the amount of fertilizer for the planned spring wheat yield. The average values of factors from the studied sample were fed to the input of the neural network model, and the yield was set. At the output, in the form of neural network responses, the required amounts of introduced nitrogen, phosphorus, and potassium fertilizers were obtained. Some results are presented in Figure 2.
The results obtained very much depend on the initial content of useful chemical elements in the soil. For example, for the sample in Table 1, the average value of nitrogen content is 309 kg per 1 ha, phosphorus content – 369, potassium – 299. Figure 3 shows the relationship between spring wheat yield and the total amount of initial content and fertilizer applied. In particular, for a given yield of 2.5 t / ha, it is required to add 28 kg of active substance per 1 ha of nitrogen, 59 kg of phosphorus, 54 kg of potassium, and 64 kg of nitrogen, 95 kg of phosphorus, 80 kg of potassium per 3 ha.
A fragment of the table of the studied data
Calculation errors on a test data set
 |
Fig. 1. The graph of the neural network model |
 |
Fig. 2. The dependence of the number of fertilizers on the planned yield |
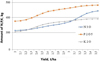 |
Fig. 3. Dependence of the total amount of the initial content and fertilizer applied on the planned yield. |
4 Conclusion
The neural network model that we developed made it possible to calculate fertilizer application doses taking into account 15 influencing factors on the planned yield. The constructed neural network model is adequate and can be used for calculating fertilizer doses for the planned levels of spring wheat, taking into account the initial content of nutrients in the soil. The above shows the theoretical significance of monitoring the regulated factors, providing the soil with nutrients for yield formation, and at the same time, indicates the vast possibility of applying the results in the agricultural practice of the Republic of Tatarstan and our country as a whole.
References
- F.Sh. Shaikhutdinov, Agrobiological basis of wheat yield formation Dicoccum Schrank (spelt) in the ancestral domain of the Republic of Tatarstan, BIO Web of Conferences, 17, 00072 (2020) DOI: https://doi.org/10.1051/bioconf/20201700072 [CrossRef] [EDP Sciences] [Google Scholar]
- V. Petrenko, T. Sheiko, R. Spychaj, O. Prysiazhniuk, L. Khudolii, Evaluation of three wheat species (Triticum aestivum L., T. spelta L., T. dicoccum (Schrank) Schuebl) commonly used in organic cropping systems, considering selected parameters of technological quality, Romanian Agricultural Research, 35, 255-264 (2018) [Google Scholar]
- F.Sh. Shaikhutdinov, R.I. Ibyatov, A.A. Valiev, Modern methods and approaches for processing information on spring wheat yield, Bulletin of Kazan State Agrarian University, 11, 3(41), 9-15 (2016) [CrossRef] [Google Scholar]
- N.G. Kiseleva, R.I. Ibyatov, Modeling taxation indicators of stands in the environment of office programs, Bulletin of Kazan State Agrarian University, 2(40) (2016) [Google Scholar]
- M.F. Amirov, A.M. Amirov, Spring durum wheat of the Volga forest-steppe (Brig, Kazan, 2018) 290 p. [Google Scholar]
- M.F. Amirov, The effect of trace elements and mineral fertilizers on the yield and quality of grain of spring wheat, Bulletin of Kazan State Agrarian University, 4(47), 5-9 (2017) [CrossRef] [Google Scholar]
- F.N. Safiollin, G.S. Minnullin, M.M. Khismatullin, S.V. Sochneva, Backgrounds of mineral nutrition of alfalfa agrocenoses and yield of the subsequent crop rotation field crop spring wheat Ekada 70 on grey forest soils of the Republic of Tatarstan, Grain Economy of Russia, 2(50), 20-33 (2017) [Google Scholar]
- A.N. Kshnikatkina, I.G. Rusyaev, Yield and grain quality of spring wheat depending on the pre-sowing treatment of seeds with complex micronutrient fertilizers and bacterial preparations, Agrochemical Bulletin, 3, 48-51 (2018) [Google Scholar]
- V.G. Kutilkin, S.N. Zudilin, Influence of the main elements of the farming system on the efficiency of using solar energy and moisture by winter wheat crops, Agriculture, 2, 19-22 (2018) [Google Scholar]
- N. Daskalova, S. Doneva, P. Spetsov, Chromosome variation and HMW glutenins in synthetic hexaploid kinds of wheat (Triticum turgidum ssp. dicoccum/Aegilops tauschii), Cereal Research Communications, 44(3), 453-460 (2016) [Google Scholar]
- V.G. Vasin, N.A. Prosandeev, Technological evaluation of grain and economic efficiency of the use of herbicides in wheat and barley crops, Bulletin of the Orenburg State Agrarian University, 3, 53-56 (2012) [Google Scholar]
- S.V. Novikova, Structural Optimization of the Neural Network Model for the Gas Turbine Engine Monitoring, Russian Aeronautics (Iz. VUZ), 59(2), 263-270 (2016) DOI 10.3103/S1068799816020185 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. The graph of the neural network model |
| In the text | |
 |
Fig. 2. The dependence of the number of fertilizers on the planned yield |
| In the text | |
 |
Fig. 3. Dependence of the total amount of the initial content and fertilizer applied on the planned yield. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.